薄板ばねについての技術情報です。
計算式を掲載しておりますのでご参考にしてください。
技術的なご質問などございましたお気軽にこちらからご連絡ください。
「こだま」がご提供できること
１）板バネの構想段階からのご相談
材質・形状・機能性
など、構想段階から対応いたします。
２）金型レス製作で、精密板金部品製作1個から
標準化された独自の金型で、初期費用ゼロで小部品製作が可能
３）約100個のリピート品、約2000個の限定製作対応
簡易金型技術、製作方法の選択で、コストパフォーマンスのご提供
４）様々な材料、豊富な在庫と材料入手
SUS系、リボン鋼、銅系、チタン系、インコネル系等
５）ｔ0.005～の箔・微細加工技術
６）精密切削加工
７）各種溶接加工
８）各種表面処理・熱処理加工
９）各種金型・治具電極製作
１０）材料分析
7.2 計算式
板バネ（板ばね）の設計上問題となることは、限られた容積の中で必要なばね荷重またはたわみを得るための形状の選定と、ばねに生ずる最大応力の位置と大きさの推定であって、比較的簡単なばね形状に対しては一般の材料力学に示されている式が利用できる。
7.2.1 直線状片持ばね
図7.1のように長方形の一端を固定したばねに荷重Ｐを図示の位置に作用させたとき、任意位置xでのたわみbxは次のように表わされる。
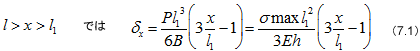
図中のｌ１は荷重作用点までの長さで、ｌは全長である。式中のＢは板の曲げこわさとよばれ、板厚がかなり厚いときは
板厚がごく薄いときは
となる。Ｅは材料の縦弾性係数、ｖはポアソン比。
ｂおよびｈはそれぞれ板幅および板厚を、またσmaxは固定端における最大曲げ応力を表わす。
荷重作用点が自由端の場合には、x＝l1＝ｌとおいて、自由端におけるたわみδを次のように表わすことができる。
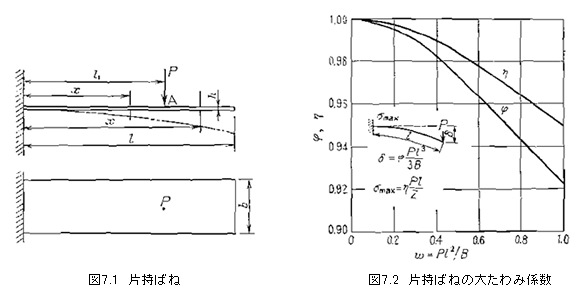
この場合δが大きくδ＞0.2ｌとなると、いわゆる大たわみとして取り扱わなければならない。
この結果たわみおよび応力は次式のように表わされ、式中のφおよびηの値は図7.2のように示される。
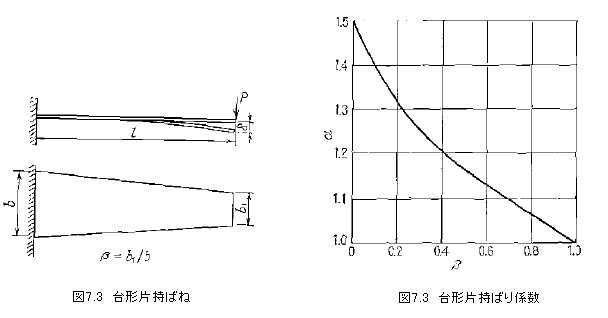
図7.3のようにばねの板厚ｈが一定で板幅が直線的に変化している場合、自由端のたわみδは、
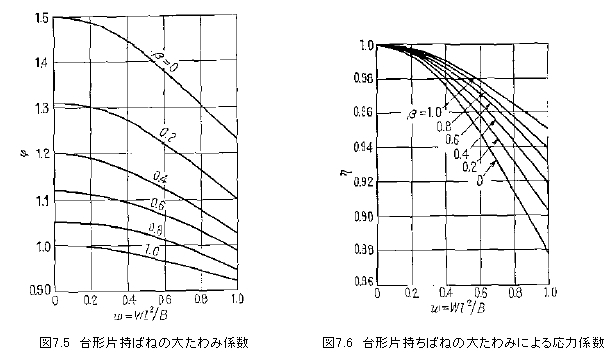
式中のαの値は、β＝ｂ1/ｂによって図7.4のように示される。
大たわみに対しては上記の式（7.6）と同様に表わされ、φおよびηの値は図7.5及び図7.6のようになる。
電気接点などに使われる図7.7に示す形状のばねで支持点Cにおける支力Pは、支持点のばね定数ｋ、作用荷重W、ばねと支持点
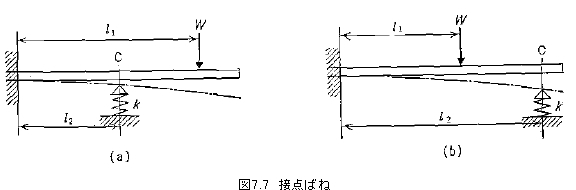
が接触したときの荷重をWcとすると次のように示される。
図7.7（a）では
図7.7（ｂ）では
図7.8のように板厚が一定で、板幅が段付けをしているばねの自由端のたわみδは
ここでδA、iAは、Pによる段付部Aのたわみとたわみ角、δBは長さｌ2、板幅ｂ2の片持はりのたわみを示す。
板厚の中心線が直線で、板幅の中心線が円弧状をしているばね図7.9に垂直荷重Pが自由端に作用したとき、任意位置φでのたわみδφは、
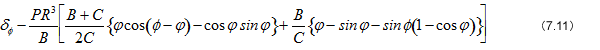
ここで、Cは板のねじりこわさを表わす。
7.2.2 円弧状片持ばね
板厚の中心線が円弧である片持ばねに荷重が作用したときのたわみを求めるには、一般にカステリアノ定型を用いる。以下はこれを利用して計算した結果をあげる。
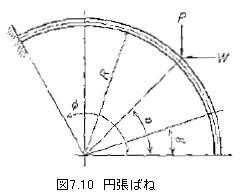
図7.10に示す形状の円弧ばねに、垂直荷重P、水平荷重Wがそれぞれ単独に中心角αの位置に作用したとき、中心角βの位置でｙ方向のたわみδｙ、ｘ方向のたわみδｘは次のようになる。
Ｐによるたわみδｙはβ＜αのとき
β>αのとき
Ｗによるたわみδｘはβ<αのとき
β>αのとき
図7.11においてはδｙ、δｘはそれぞれ次のようになる。
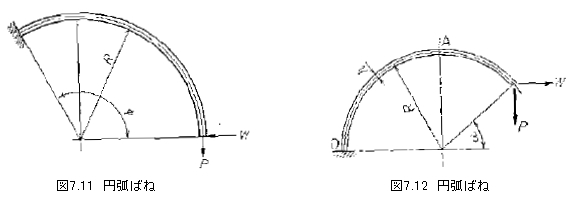
図7.12の場合は
Ｐによる最大応力σmaxはつねに固定端で起こり
Wによる最大応力はα<30°では図7.12のA点で、α>30°では固定端で起こり
図7.13に示す円輪状のばねは、上下対称であるので図7.12の形状のたわみの2倍が全たわみとなる。
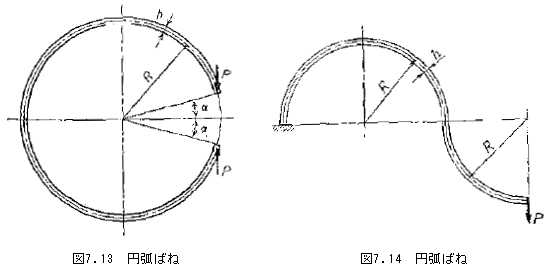
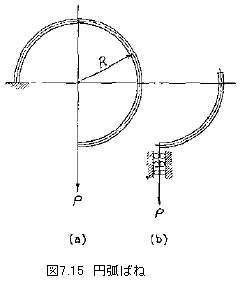図7.14に示す半円と1/4円との組合せばねでは、自由端におけるたわみは
最大応力は固定端に生じ
図7.15（a）に示す形状の自由端のたわみは
図7.15（ｂ）では垂直方向は自由であるが、水平方向が拘束されている場合
最大応力は両者とも
7.2.3 円弧と直線部分とを有するばね
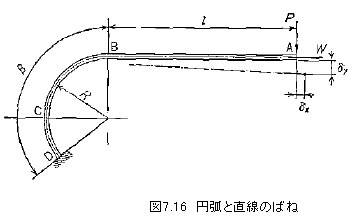
図7.16のように直線部ABと円弧部BDとが組み合わされて、一端Dが固定され他端Aに垂直荷重Pまたは水平荷重Wが作用したときδｙ、δｘはそれぞれ次のようになる。
Pが作用する場合
β＝π/2の場合には
Wが作用する場合は
式中のλはλ＝ｌ/Rを表わす。
最大応力はβ≦ｘ/2では固定端において生じ、β>ｘ/2ではC点に生じる。
図7.17は図7.16に示したばねを2つ組み合わせたもので、荷重作用方向のたわみδは式（7.28）で得られたたわみの2×sin2β倍となる。
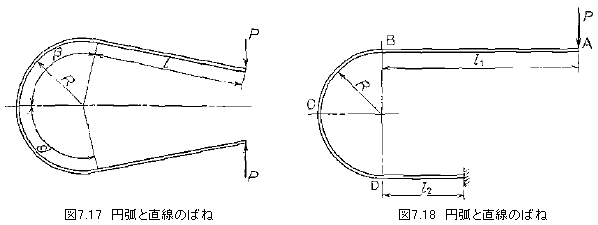
図7.18に示した直線部と円弧部を有したばねのA端のたわみは
ここでλ＝l1/R、μ＝ｌ2/Rを表わす。
最大曲げ応力はC点において生じ、
l1<l2のときは(l2-l1)>(l1+R)の場合、最大応力は固定端で起こり(l2-l1)<(l1+R)ではC点で生じ、式（7.36）と同様に表わされる。
λ=μのときは
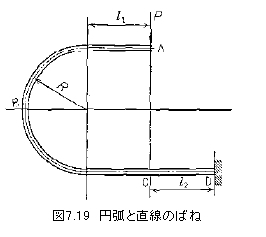図7.19の形状の場合はAC部とCD部とを分割して、式（7.30）のたわみの2倍と式（7.5）のたわみおのおの計算し、加え合わせることによってA部のたわみを得ることができる。
図7.20のように直線部が固定され円弧部のA端に荷重が作用したとき、A端の垂直たわみδyおよび水平たわみδｘは、λ＝ｌ/Rとして荷重Pが作用したとき
荷重Wが作用したとき
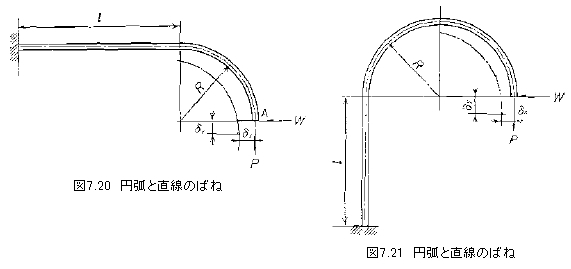
図7.21の形状では荷重Pが作用したとき
Wが作用したとき
ただしλ＝ｌ/Rを表わす。
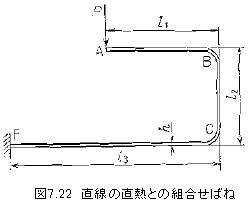曲率半径の小さい円弧と直線を組み合わせた形状（図7.22）のばねでは、円弧部の半径を無視してたわみは次式で表わせる。
最大応力はl1＞（l1/2）のときBC部に
l1＜（l1/2）のときは固定端において
